Aprenda Sistemas Lineares com C++

Um sistema linear é um conjunto de equações lineares com as mesmas variáveis. Sua solução consiste em encontrar valores para as variáveis que satisfaçam todas as equações simultaneamente.

Exemplo 01

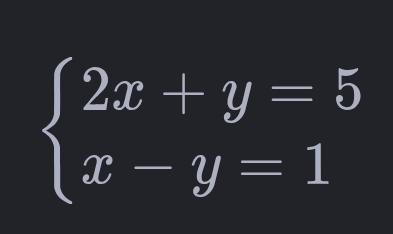
Sistema Linear Exemplo

A solução desse sistema é x = 2 e y = 1, pois substituindo esses valores nas duas equações, ambas são verdadeiras.

Solucionando com C++:

#include <iostream>
#include <cmath>

auto solve = [](double a1, double b1, double c1,
    double a2, double b2, double c2,
    double &x, double &y) -> void {

  // Calculando o determinante
  double det = a1 * b2 - a2 * b1;

  if(std::abs(det) < 1e-10){
    std::cout << "Sistema não tem solução única (determinante zero).\n";
    return;
  }

  // Aplicando a regra de Cramer
  x = (c1 * b2 - c2 * b1) / det;
  y = (a1 * c2 - a2 * c1) / det;
};

int main(){
  double a1 = 2, b1 = 1, c1 = 5;  // Equação 1: a1*x + b1*y = c1
  double a2 = 1, b2 = -1, c2 = 1; // Equação 2: a2*x + b2*y = c2

  double x, y;

  solve(a1, b1, c1, a2, b2, c2, x, y);

  std::cout << "x = " << x << '\n';
  std::cout << "y = " << y << '\n';
}

Você também poderia resolver manualmente somando as duas equações:

2x + y = 5
 x - y = 1
---------
3x     = 6  => x = 2

Substituindo x=2 na segunda equação:
2 - y = 1 => y = 1

Mas a implementação em C++ apresentada é mais geral e pode ser usada para qualquer sistema linear 2x2.

Representação Matricial

Podemos escrever um sistema linear na forma matricial A • X = B, onde:

A = Matriz dos coeficientes
X = Vetor das variáveis
B = Vetor dos termos independentes

Exemplo:
O sistema desse Exemplo 01 pode ser escrito como:

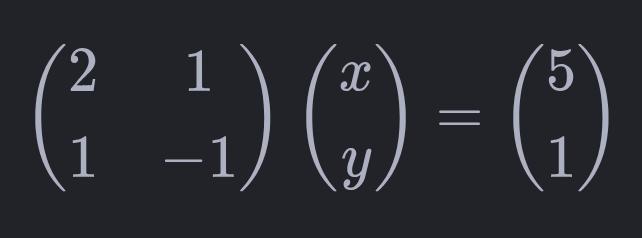
Representação Matricial

Métodos de Resolução

a) Método da Substituição

Isola-se uma variável em uma equação.
Substitui-se essa expressão na outra equação.

Da Equação 2, isolamos: x: x = 1 + y
Substituímos na Equação 1:

2(1 + y) + y = 5  
2 + 2y + y = 5  
3y = 3  
y = 1

Substituindo y = 1 em x = 1 + y: x = 2

Solução: (2, 1).

Método da Adição (Eliminação)

Consiste em somar ou subtrair as equações para eliminar uma variável.

Somamos as duas equações:

(2x + y) + (x - y) = 5 + 1  
3x = 6  
x = 2

Substituímos ( x = 2 ) em uma das equações:

2 - y = 1  
y = 1

Solução: (2, 1).

Para usar o Método de Cramer você precisa entender: Determinantes.

Classificação dos Sistemas Lineares**

Possível e Determinado (SPD): Tem uma única solução D ≠ 0.
Possível e Indeterminado (SPI): Tem infinitas soluções (equações linearmente dependentes).
Impossível (SI): Não tem solução (equações contraditórias).

Exemplo 02

Resolver esse sistema linear com C++:

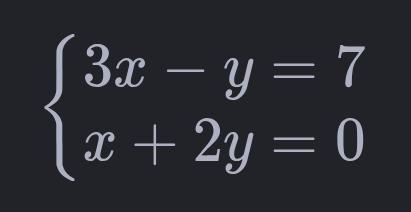
Exemplo 02

Solução:

#include <iostream>
#include <cmath>

auto solve = [](double a1, double b1, double c1,
    double a2, double b2, double c2,
    double &x, double &y) -> void {
  double det = a1 * b2 - a2 * b1;

  if (std::abs(det) < 1e-10) {
    std::cout << "Sistema não tem solução única (determinante zero).\n";
    return;
  }

  x = (c1 * b2 - c2 * b1) / det;
  y = (a1 * c2 - a2 * c1) / det;
};

int main() {
  // Sistema:
  // 3x - y = 7
  // x + 2y = 0
  double a1 = 3, b1 = -1, c1 = 7;
  double a2 = 1, b2 = 2,  c2 = 0;

  double x, y;
  solve(a1, b1, c1, a2, b2, c2, x, y);

  std::cout << "x = " << x << '\n';
  std::cout << "y = " << y << '\n';
}

Exemplo proposto para você solucionar

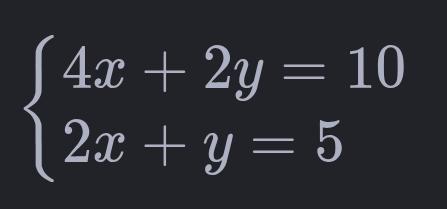
Exemplo proposto

Resposta:

+ O sistema tem infinitas soluções. + É um sistema possível e indeterminado. A solução geral pode ser expressa, por exemplo, em termos de um parâmetro t:

x = (5 - t) / 2
y = t

Links úteis com exercícios propostos e com respostas:

PDFs:

Sites:

matematica cpp