Aprenda Matrizes e Determinantes com C++

Nesse artigo recapitularemos conceitos fundamentais sobre Matrizes e Determinantes.

Matriz

Uma explicação rápida sobre Matriz Matemática é que ela serve para organizar dados numéricos(criando uma tabela) para facilitar a leitura e organização dos dados para solucionar problemas de forma mais fácil.

As Matrizes são utilizadas em diversas áreas:

Matemática;
Computação(Inteligência Artificial, tratamento de imagens,…);
Engenharia;
Economia;
Biologia;

E entre diversas outras.

O conceito em linhas gerais é: Uma matriz é uma tabela retangular de números (ou expressões) organizados em linhas e colunas., sua representação se parece com isso:

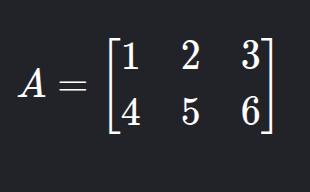
Essa matriz tem uma ordem de: 2x3 (2 linhas(horizontal) e 3 colunas(vertical)), nas representações de matrizes sempre começamos informando as linhas.

Outra observação sobre essa matriz é que ela possui a explicação: A = [aij]<sub>mxn</sub>, isso quer dizer que, por exemplo:

O número 1 está na 1º linha(m) e na 1º coluna(n), logo, a representação a_ij dele é: a₁₁ e assim por diante.

Convertendo todos para a_ij, seria:

Essa mesma matriz em C++ podemos usar o std::vector ou std::array:

Use std::vector<std::vector<int>> se quiser algo dinâmico e flexível.
Use std::array<std::array<int, 3>, 2> se as dimensões forem fixas e conhecidas em tempo de compilação. Nunca use std::list para matrizes. Ela não tem acesso aleatório eficiente.

Exemplos:

Com std::vector:

std::vector<std::vector<int>> A = {
    {1, 2, 3},
    {4, 5, 6}
};

Com std::array:

std::array<std::array<int, 3>, 2> A = { {
    {1, 2, 3},
    {4, 5, 6}
} };

Qual usar?

Use std::vector se for alterar tamanho em tempo de execução.
Use std::array para desempenho máximo com tamanho fixo.

Construção de matrizes

Suponhamos que você está prestando um concurso e possui esse enunciado:

Construa a matriz B = [a_ij]_2x3 tal que a_ij = (i + j)².

Solução:

a_ij = (i + j)² => a₁₁ = (0 + 0)² => a₁₁ = 0.

Faça para os demais

A solução para todos em C++ utilizando std::array, já que a matriz é de tamanho fixo 2x3:

 
#include <array>
#include <iostream>

int main() {
  std::array<std::array<int, 3>, 2> B;

  for (int i = 0; i < 2; ++i) {
    for (int j = 0; j < 3; ++j) {
      B[i][j] = (i + j) * (i + j);
    }
  }

  // Exibe a matriz
  for (const auto& row : B) {
    for (int val : row) {
      std::cout << val << " ";
    }
    std::cout << "\n";
  }

  return 0;
}

Se quiser com std::vector, troca por:

 
std::vector<std::vector<int>> B(2, std::vector<int>(3));

O resto do código é igual.

O resultado será:

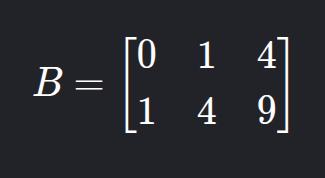
Tipos de Matrizes

1. Matriz Quadrada

Descrição: Número de linhas igual ao de colunas (nxn).
Exemplo:

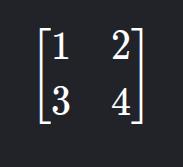
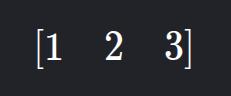
2. Matriz Linha

Descrição: Apenas uma linha.
Exemplo:

3. Matriz Coluna

Descrição: Apenas uma coluna.
Exemplo:

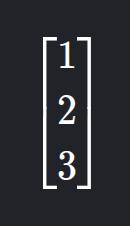
4. Matriz Nula

Descrição: Todos os elementos são zero.
Exemplo:

5. Matriz Identidade

Descrição: Diagonal principal com 1 e o resto 0. Denotada por I_n.
Exemplo:

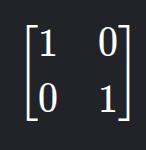
6. Matriz Diagonal

Descrição: Apenas a diagonal principal pode ter valores diferentes de zero.
Exemplo:

7. Matriz Escalar

Descrição: Matriz diagonal com todos os valores da diagonal iguais.
Exemplo:

8. Matriz Simétrica

Descrição: A = A^T, ou seja, é igual à sua transposta.
Exemplo:

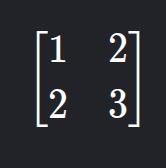
9. Matriz Antissimétrica (ou Skew-Simétrica)

Descrição: A^T = -A. Diagonal principal é sempre zero.
Exemplo:

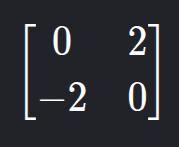
10. Matriz Triangular Superior

Descrição: Todos os elementos abaixo da diagonal principal são zero.
Exemplo:

11. Matriz Triangular Inferior

Descrição: Todos os elementos acima da diagonal principal são zero.
Exemplo:

12. Matriz Transposta

Descrição: Linhas viram colunas. Denotada A^T.
Exemplo:

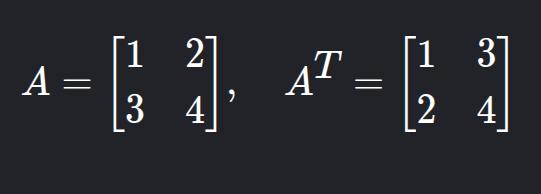
13. Matriz Oposta

Descrição: Todos os elementos multiplicados por -1.
Exemplo:

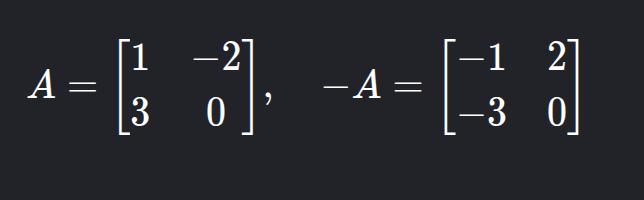
14. Matriz Retangular

Descrição: Número de linhas diferente do número de colunas.
Exemplo:

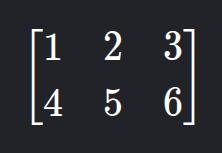
Cálculos de Matrizes

Operações aritméticas(algébricas ou matriciais) com Matrizes.

a) Adição e Subtração

Só é possível se as matrizes tiverem a mesma ordem.

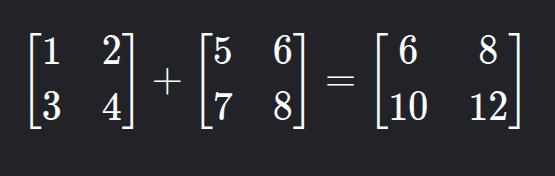
Ou seja, 1 + 5 = 6, 2 + 6 = 8 e assim por diante.

Em C++:

 
#include <array>
#include <iostream>

int main() {
  std::array<std::array<int, 2>, 2> A = { { {1, 2}, {3, 4} } };
  std::array<std::array<int, 2>, 2> B = { { {5, 6}, {7, 8} } };
  std::array<std::array<int, 2>, 2> C;

  for (int i = 0; i < 2; ++i){
    for (int j = 0; j < 2; ++j){
      C[i][j] = A[i][j] + B[i][j];
    }
  }

  for (auto& row : C){
    for (int v : row){
      std::cout << v << (v == row.back() ? '\n' : ' ');
    }
  }
}

b) Multiplicação por Escalar

Multiplica-se cada elemento por um número real (escalar).

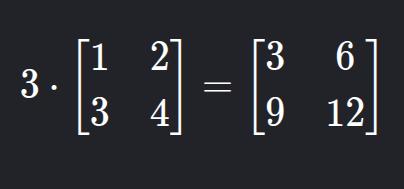
Ou seja, 3 x 1 = 3, 3 x 2 = 6 e assim por diante.

Em C++:

 
#include <array>
#include <iostream>

int main() {
  std::array<std::array<int, 2>, 2> A = { { {1, 2}, {3, 4} } };
  std::array<std::array<int, 2>, 2> B;
  int escalar = 3;

  for (int i = 0; i < 2; ++i){
    for (int j = 0; j < 2; ++j){
      B[i][j] = escalar * A[i][j];
    }
  }

  for (auto& row : B){
    for (int v : row){
      std::cout << v << (v == row.back() ? '\n' : ' ');
    }
  }
}

c) Multiplicação de Matrizes

O número de colunas da primeira matriz deve ser igual ao número de linhas da segunda.

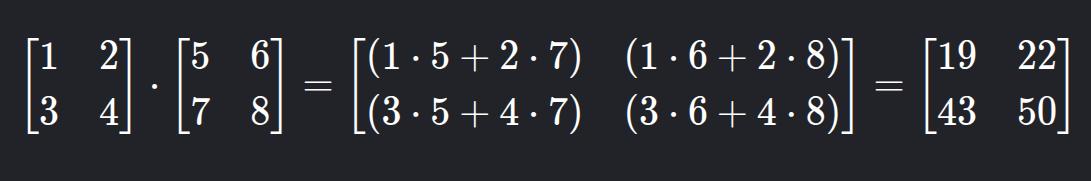
Em C++:

 
#include <array>
#include <iostream>

int main() {
  std::array<std::array<int, 2>, 2> A = { { {1, 2}, {3, 4} } };
  std::array<std::array<int, 2>, 2> B = { { {5, 6}, {7, 8} } };
  std::array<std::array<int, 2>, 2> C = {};

  for (int i = 0; i < 2; ++i){
    for (int j = 0; j < 2; ++j){
      for (int k = 0; k < 2; ++k){
        C[i][j] += A[i][k] * B[k][j];
      }
    }
  }

  for (auto& row : C){
    for (int v : row){
      std::cout << v << (v == row.back() ? '\n' : ' ');
    }
  }
}

Determinantes

O determinante é um número associado apenas a matrizes quadradas, útil para resolver sistemas lineares e verificar se uma matriz é invertível.

IMPORTANTE: Na representação de matrizes usamos colchetes: [ ], mas em determinantes usamos barras verticais, exemplo: | |.

3.2 Cálculo do Determinante

a) Matriz `2x2`

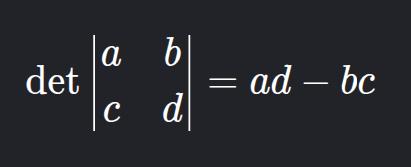
Exemplo:

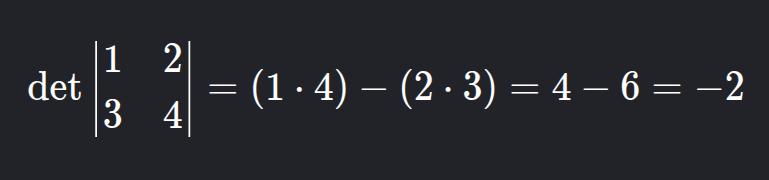
Em C++:

 
#include <iostream>

int main(){
  int a = 1, b = 2;
  int c = 3, d = 4;

  int det = a * d - b * c;

  std::cout << det << '\n';
}

b) Matriz `3x3` (Regra de Sarrus)

A Regra de Sarrus consiste em adicionar a 1º e a 2º coluna para o lado direito da matriz determinante e traçar diagonais(a partir dos números da primeira LINHA), exemplo:

Isso para uma matriz 3x3.

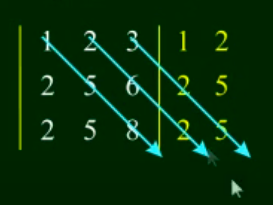
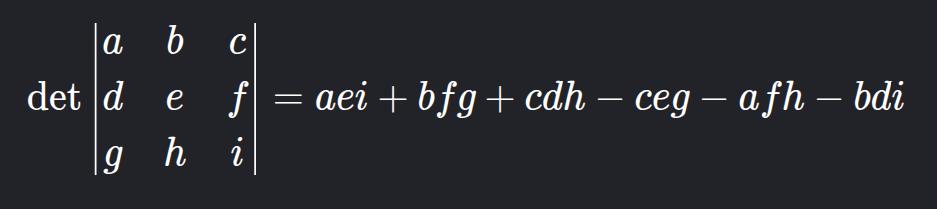
Exemplo:

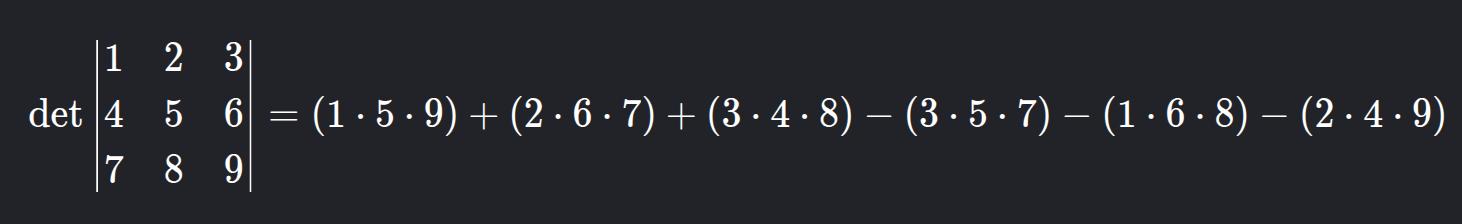
= 45 + 84 + 96 - 105 - 48 - 72 = 0

Em C++:

 
#include <iostream>

int main(){
  int a11 = 1, a12 = 2, a13 = 3;
  int a21 = 4, a22 = 5, a23 = 6;
  int a31 = 7, a32 = 8, a33 = 9;

  int det = 
    a11 * a22 * a33 +
    a12 * a23 * a31 +
    a13 * a21 * a32
    - a13 * a22 * a31
    - a11 * a23 * a32
    - a12 * a21 * a33;

  std::cout << det << '\n';
}

3.3 Propriedades dos Determinantes

Se uma linha ou coluna for toda zero, det = 0.
Se duas linhas ou colunas forem iguais, det = 0.
det(A x B) = det(A) x det(B).

4. Aplicações

Sistemas Lineares: Resolver equações usando a Regra de Cramer.
Matriz Inversa: Uma matriz A é invertível se det(A) ≠ 0.

5. Exercício

Calcule o determinante:

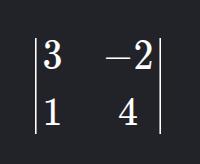
Em C++:

 
#include <iostream>

int main(){
  int a = 7, b = 3;
  int c = -2, d = 4;

  int det = a * d - b * c;

  std::cout << det << '\n';
}

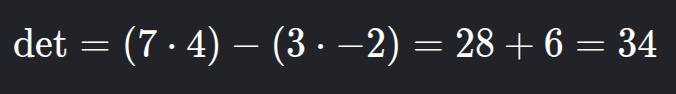
Resposta: 14.

Links úteis

matematica cpp